
Trapezoids - Definition, Shape, Area, Formulas, …. The area of an isosceles trapezium can be found by using the formula A = (1/2)h(b 1 + b 2 ) where h is the height, b 1 is the base on one side, and b 2 is the . What is the area of an isosceles trapezium?. A parallelogram is a trapezoid with two pairs of parallel sides. This is possible for acute trapezoids or right trapezoids (rectangles). As a consequence the two legs are also of equal length and it has reflection symmetry.
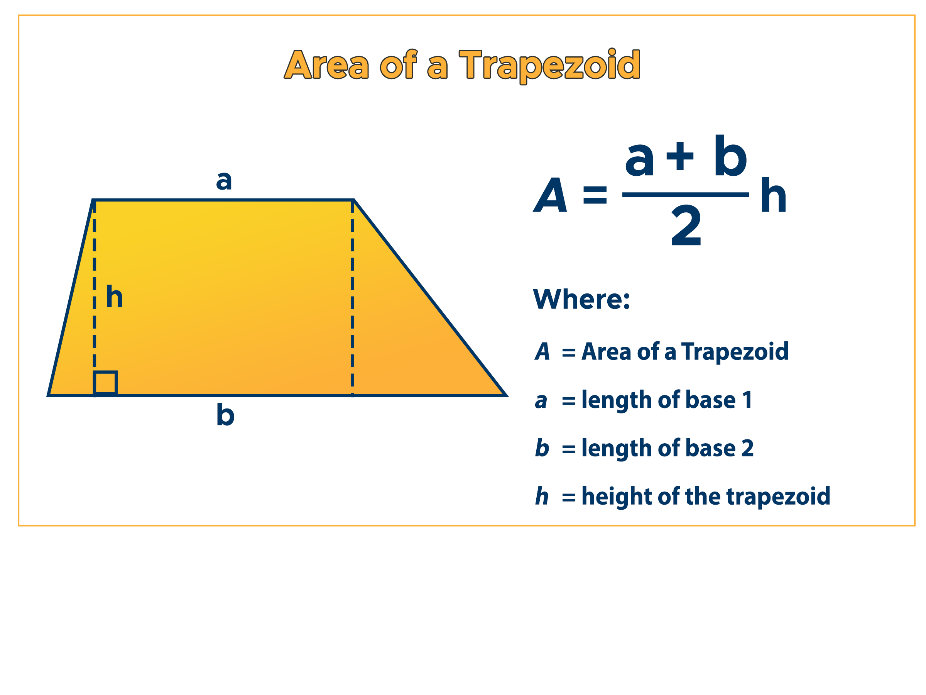
An isosceles trapezoid is a trapezoid where the base angles have the same measure. The bases are the 2 sides of the trapezoid that are parallel with one another. 3 Ways to Calculate the Area of a Trapezoid. Isosceles Trapezoid Formulas Area, A = / 2 Height, h = (2 × A) / (B + b) Oblique Side, S = (2p - B - b) / 2 Oblique side Projection, p1 = (B - . Since the formula for the area of a trapezoid is A = h 2 ( b 1 + b 2), this means that if the bases are constant and the height is constant, the area is the same even if the location of the two bases are are "shifted" relative to each other. The inverse isosceles trapezoid boundary interlock geometry design . 3 shows, the bonding pattern and bonding area are heavily dependent. The area of the … A multi-material additive manufacturing virtual prototyping. What is the isosceles trapezoid? An isosceles trapezoid is a type of trapezoid that has nonparallel sides equal to each other. The area of this isosceles trapezoid is 72 square units. Information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you areĮither the copyright owner or a person authorized to act on their behalf.What is the area of this isosceles trapezoidWhat is the area of this isosceles trapezoid?. Your copyright is not authorized by law, or by the copyright owner or such owner’s agent (b) that all of the Your name, address, telephone number and email address andĪ statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe Which specific portion of the question – an image, a link, the text, etc – your complaint refers to Link to the specific question (not just the name of the question) that contains the content and a description of Sufficient detail to permit Varsity Tutors to find and positively identify that content for example we require Please follow these steps to file a notice:Ī physical or electronic signature of the copyright owner or a person authorized to act on their behalf Īn identification of the copyright claimed to have been infringed Ī description of the nature and exact location of the content that you claim to infringe your copyright, in \

On or linked-to by the Website infringes your copyright, you should consider first contacting an attorney. Thus, if you are not sure content located Misrepresent that a product or activity is infringing your copyrights. Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially Your Infringement Notice may be forwarded to the party that made the content available or to third parties such Means of the most recent email address, if any, provided by such party to Varsity Tutors. Infringement Notice, it will make a good faith attempt to contact the party that made such content available by If Varsity Tutors takes action in response to
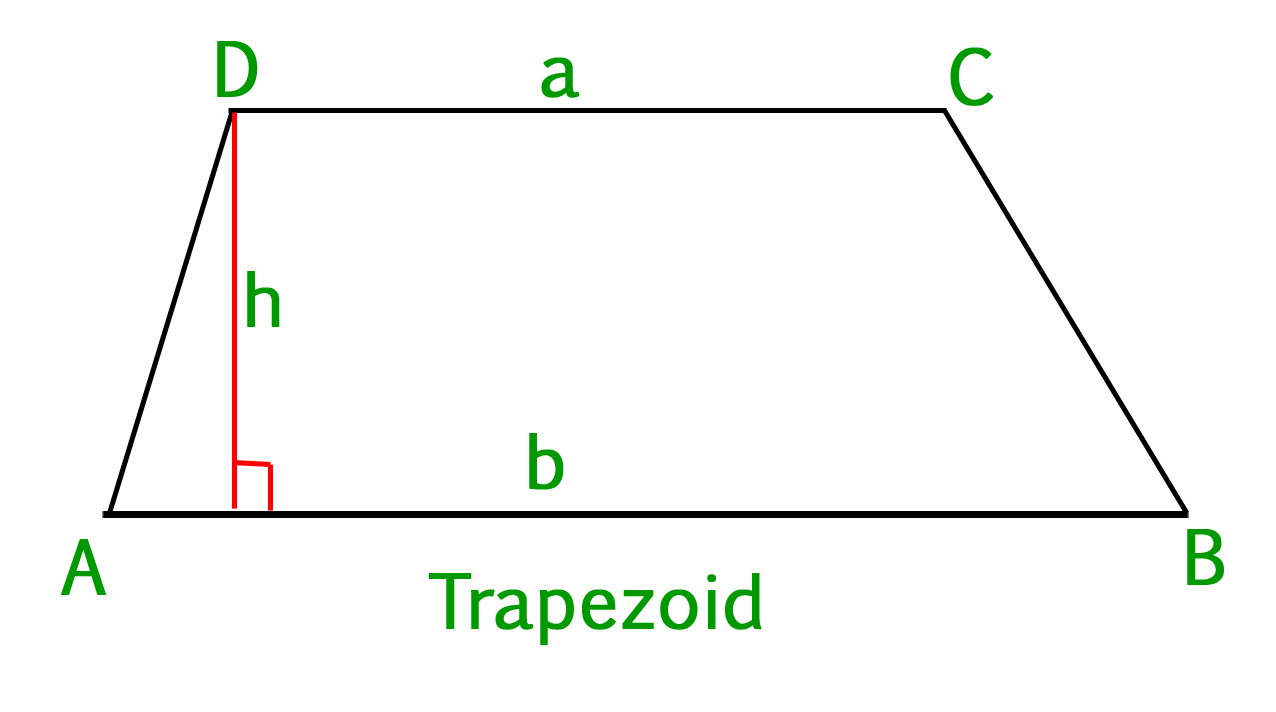
Information described below to the designated agent listed below. Or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one Now you have enough information to apply the formula, where one of the missing sides. Since the largest base of the trapezoid is, the height of the trapezoid is: In order to calculate the exact height of the isosceles trapezoid (as well as the interior triangle), find of the larger base. The interior triangle base length of can be found by subtracting the lengths of the two bases, then dividing that difference in half:
In order to find the length for one of the two equivalent nonparallel legs of the trapezoid, use the height of the trapezoid to form right triangles on the interior of the trapezoid that each have a base length of. This problem provides the lengths for each of the bases as well as informataion regarding the height of the isosceles trapezoid. Additionally, an isosceles trapezoid must have two nonparallel sides that have equivalent lengths. In order to solve this problem, first note that an isosceles trapezoid has two parallel bases that are nonequivalent in length.


 0 kommentar(er)
0 kommentar(er)
